Tag: modelos matemáticos

Para ver a segunda parte clique aqui

Expressões regulares – Toda Linguagem Regular pode ser descrita por uma expressão simples denominada Expressão Regular. Trata-se de um formalismo denotacional também considerado gerador, pois pode-se inferir como construir (“gerar”) as palavras de uma linguagem. É uma maneira de representar uma linguagem formada pela justaposição dos símbolos do alfabeto separados pelos símbolos de união ou concatenação.

Linguagem – Conjunto de palavras

L1 = {0,01,11} ou L2 = {111,000}

Operações

L1UL2 = {0,01,11,111,000}

L1L2 = {0111,0000,0011,…}

L1*={0000,010101,…)

Linguagens Regulares – São aquelas que podem ser representadas por expressão regular ou autômatos.

Exemplos:

• L=Cadeias que possuem apenas um 0 E={0,1}
  • 1*01*
• L=Cadeias que possuem todas as strings binárias E={0,1}
  • (0U1)*
• L=Cadeias que possuem todas as strings binárias exceto o vazio E={0,1}
  • (oU1)⁺
• L=Cadeias que começam com aa e terminam com bb E={a,b}
  • aa(aUb)*bb
• L=Cadeias que começam ou terminam com bb E={a,b}
  • bb(aUb)*U(aUb)*bb

Por definição, uma linguagem é Regular se, e somente se, é possivel construir um Autômato Finito (Determinístico, Não-Determinístico ou com Movimentos Vazios), que reconheça a linguagem.

Transformação de Autômato/ER

1. Incluir dois estados ( um inicial, que aponta para o inicial antigo por E(movimento vazio), e um estado final, todos os finais antigos do autômato deixam de ser finais e apontam por E para o novo).
2. Avaliar dois a dois os estados na tentativa de eliminar um terceiro.

Hierarquia de Chomsky

É a classificação de gramáticas formais descrita em 1959 pelo linguista Noam Chomsky. Esta classificação possui 4 níveis (Descritos na figura ao lado), sendo que os dois últimos níveis (os níveis 2 e 3) são amplamente utilizados na descrição de linguagem de programação e na implementação de interpretadores e compiladores. Mais especificamente, o nível 2 é utilizado em análise sintática (computação) e o nível 3 em análise léxica.

A classificação das gramáticas começa pelo tipo 0, com maior nível de liberdade em suas regras, e aumentam as restrições até o tipo 3. Cada nível é um super conjunto do próximo. Logo, uma gramática de tipo n é conseqüentemente uma linguagem de tipo n-1.

• Linguagem tipo 3: Regular
  • Reconhecida por um autômato finito
  • Representada por uma expressão regular
• Linguagem tipo 2: Livre de contexto
  • Reconhecida por um autômato de pilha
• Linguagem tipo 1: sensível ao contexto
• Linguagem tipo 0: Irrestrita
  • Máquina de Turing

Lema do Bombeamento

Diz que se pegarmos uma cadeia de tamanho maior do que a quantidade de estados do autômato, existe um pedaço dessa cadeia que pode ser bombeada (repetida em um looping) de forma que a cadeia gerada ainda pertence a linguagem.

Isso significa que existe um looping dentro do autômato. O lema do Bombeamento serve para provar que uma linguagem “NÃO” é regular. A demonstração de que uma linguagem é regular é feita através da criação de um autômato ou expressão regular.

Não é regular

-Afirme que é regular

-Escolha uma que você ache que não é regular

-Bombear

-Provar que não é regular.

O que foi descrito neste artigo é somente o começo dos estudos das linguagens formais. Foi dividido em 3 partes, é possível acessar a segunda parte clicando aqui, e a primeira parte clicando aqui. O artigo foi baseado no livro: Linguagens Formais e Autômatos, Série Livros Didáticos Segunda edição, de Paulo Fernando Blauth Menezes, com alguns pedaços de texto retirados da Wikipedia.

Para ver a primeira parte clique aqui

Linguagens Regulares – Sistemas de Estados Finitos:

Um Sistema de Estados Finitos é um modelo matemático de sistema com entradase e saídas discretas. Pode assumir um número finito e pré-definido de estados. Cada estado resume somente as informações do passado necessárias para determinar as ações para a próxima entrada.

Autômato Finito – AFD (Autômato Finito Determinístico) é uma 5-upla:

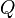• é um conjunto finito não vazio de estados do autômato;
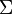• é um conjunto de símbolos, denominado alfabeto de entrada do autômato;
• é a função de transição de estados do autômato e seu papel é o de indicar as transições possíveis em cada configuração do autômato. Esta função fornece para cada par “estado e símbolo de entrada” um novo estado para onde o autômato deverá mover-se.
• é denominado estado inicial do autômato finito. É o estado para o qual o reconhecedor deve ser levado antes de iniciar suas atividades.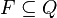
• é um subconjunto do conjunto Q dos estados do autômato, e contém todos os estados de aceitação ou estados finais do autômato finito. Estes estados são aqueles em que o autômato deve terminar o reconhecimento das cadeias de entrada que pertencem à linguagem que o autômato define. Nenhuma outra cadeia deve ser capaz de levar o autômato a qualquer destes estados.

Autômato Finito Não-Determinístico (AFN) – Autômatos finitos não determinísticos diferem dos Autômatos finitos determinísticos quanto à regra de transição entre estados. Dada uma combinação de um estado atual e um símbolo de entrada, pode não haver estados especificados para os quais o estado atual deve conduzir o processamento, bem como pode haver vários estados resultantes da leitura do símbolo. Portanto, para uma função de transição ? definida em , o seu valor não deve ser um elemento de Q (como acontece com os autômatos determinísticos), mas um subconjunto de Q (incluindo o conjunto vazio). Ou seja, o processamento de leva à um conjunto de estados em que a máquina pode legalmente se encontrar após estar em um estado q lendo um símbolo de entrada a.

Equivalência entre AFD e AFN – Embora um AFN seja somente um acréscimo ao AFD, na verdade não aumenta seu poder computacional, sendo assim, para cada AFN é possível construir um AFD equivalente que realiza o mesmo processamento. O contrário também é verdadeiro.

Autômato Finito com Movimentos Vazios – Movimentos vazios constituem uma generalização dos modelos de máquinas não-determinística, é um movimento determinado por uma simples mudança de estado.  Uma das vantagens dos autômatos Finitos com Movimentos Vazios no estudo das linguagens Formais é o fato de facilitar algumas construções e demonstrações relacionadas com os autômatos.

Equivalência entre AFN e AFe – Analogamente ao não-determinístico, os movimentos vazios não aumentam o poder computacional dos autõmatos finitos. Assim, para cada AFe, é possível construir um AFN que realiza o mesmo processamento. O contrário é trivialmente verdadeiro.

Minimização de um autômato Finito

– Alguns autômatos possuem estados que são funcionalmente os mesmos. O algorítmo de minimização tem como objetivo unir estes estados em um único.

Pré-requisitos do algorítmo de Minimização

• O autômato deve ser determinístico;
• Todos os estudos devem ser alcançados iniciando do estado inicial;

Algorítmo

• Construa uma tabela, marcando os elementos que são por definição funcionalmente diferentes (estado inicial e final)
• Dois a dois, os outros estados marcados e que são funcionalmente diferentes.
• Unir  os estados equivalentes.

Com estes conceitos básicos podemos passar para o estudo das Expressões Regulares

Autômatos finitos não determinísticos diferem dos Autômatos finitos determinísticos quanto à regra de transição entre estados. Dada uma combinação de um estado atual e um símbolo de entrada, pode não haver estados especificados para os quais o estado atual deve conduzir o processamento, bem como pode haver vários estados resultantes da leitura do símbolo. Portanto, para uma função de transição ? definida em , o seu valor não deve ser um elemento de Q (como acontece com os autômatos determinísticos), mas um subconjunto de Q (incluindo o conjunto vazio). Ou seja, o processamento de leva à um conjunto de estados em que a máquina pode legalmente se encontrar após estar em um estado q lendo um símbolo de entrada a. Assim, podemos definir um autômato finito não determinístico matematicamente como se segue.